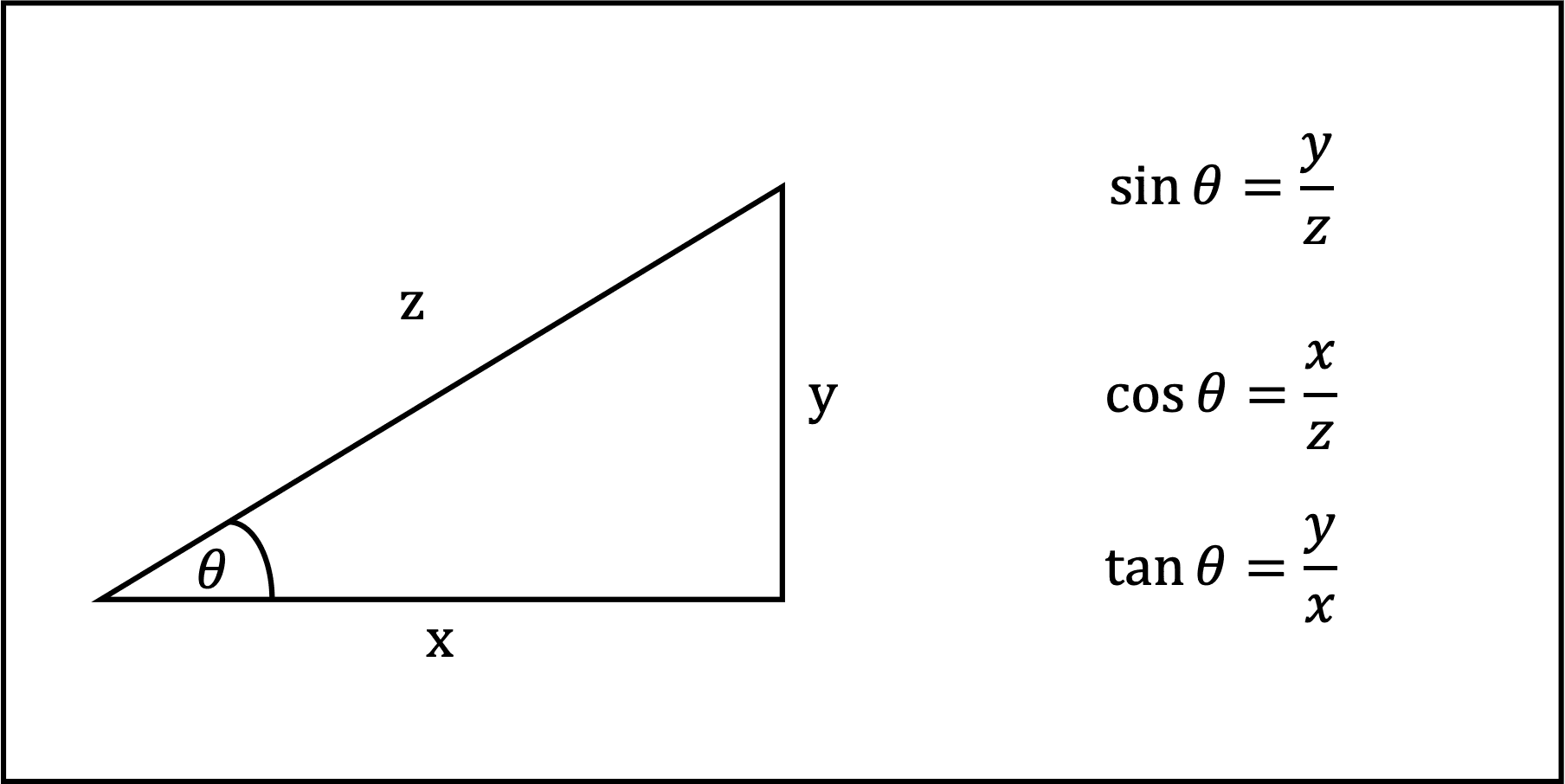
Trigonometric (Sin Cos Tan) Table 0360 Degrees (Downloadable) and How to Learn from It
In Trigonometry, different types of problems can be solved using trigonometry formulas. These problems may include trigonometric ratios (sin, cos, tan, sec, cosec and cot), Pythagorean identities, product identities, etc. Some formulas including the sign of ratios in different quadrants, involving co-function identities (shifting angles), sum & difference identities, double angle identities.
Sine, Cosine, Tangent, explained and with Examples and practice identifying opposite, adjacent
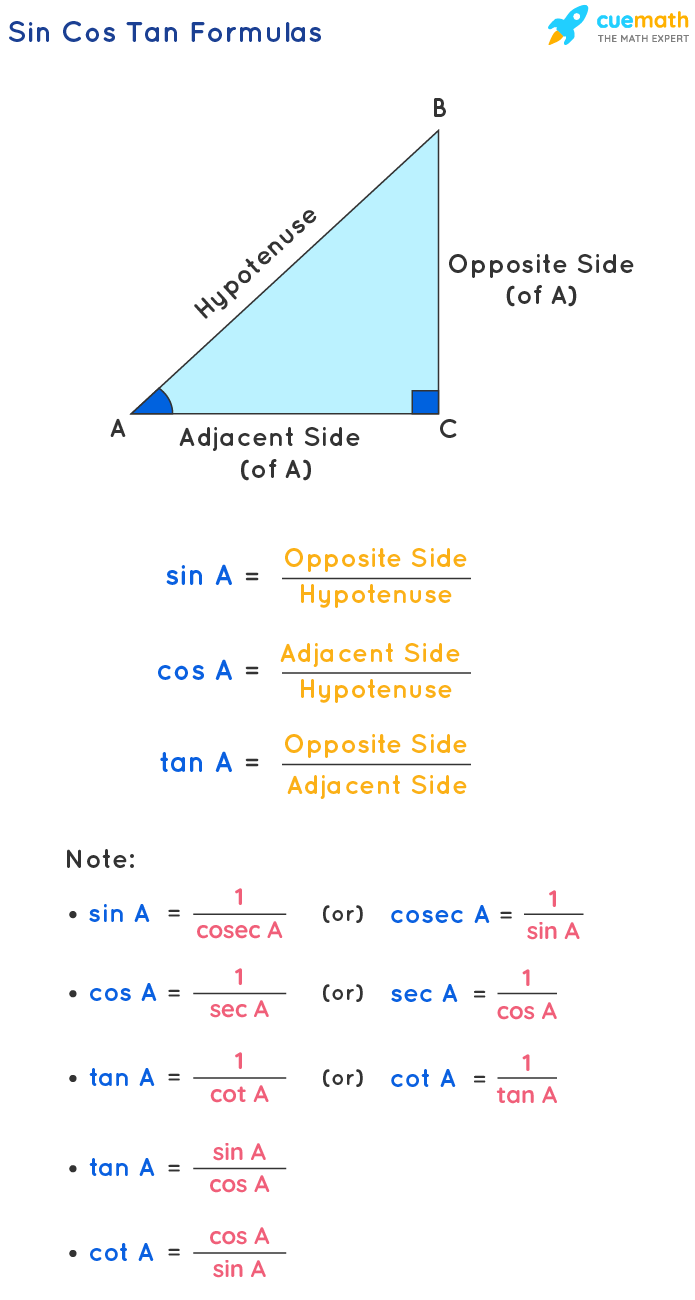
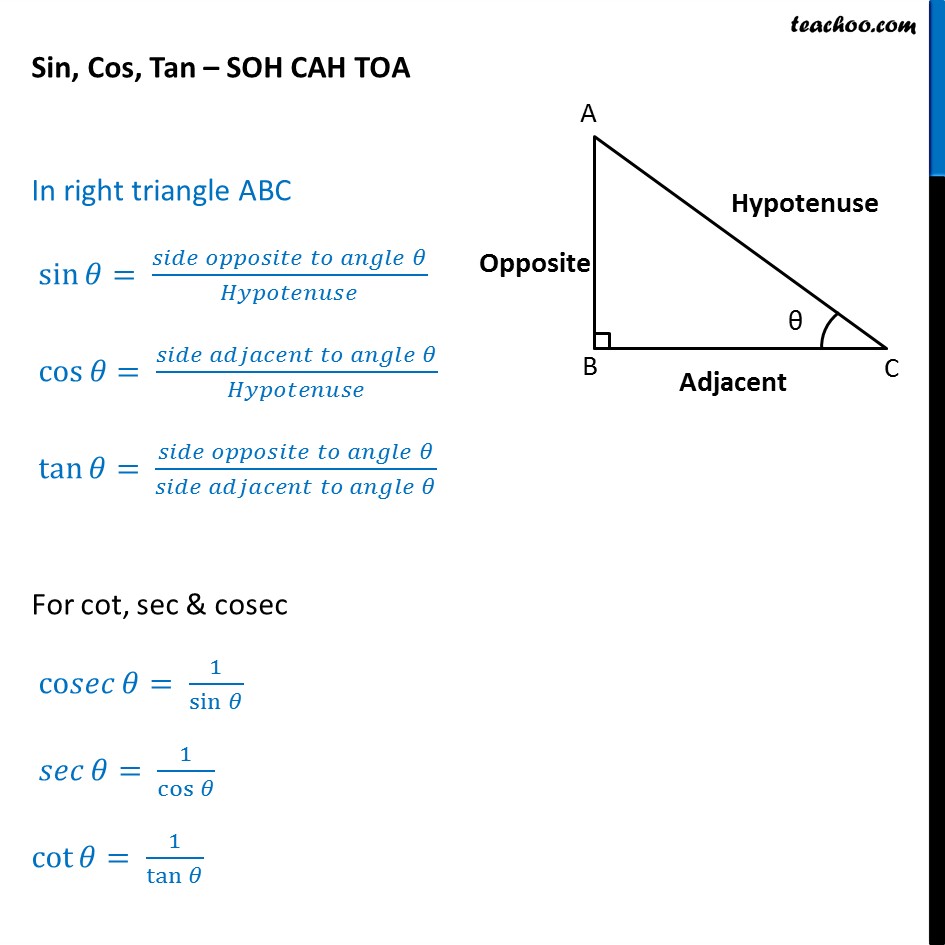
Sin Cos Tan Formula. The three ratios, i.e. sine, cosine and tangent have their individual formulas. Suppose, ABC is a right triangle, right-angled at B, as shown in the figure below: Now as per sine, cosine and tangent formulas, we have here: Sine θ = Opposite side/Hypotenuse = BC/AC; Cos θ = Adjacent side/Hypotenuse = AB/AC

Trigonometry
To calculate sine, cosine, and tangent in a 3-4-5 triangle, follow these easy steps: Place the triangle in a trigonometric circle with an acute angle in the center. Identify the adjacent and opposite catheti to the angle. Compute the results of the trigonometric functions for that angle using the following formulas: sin (α) = opposite.

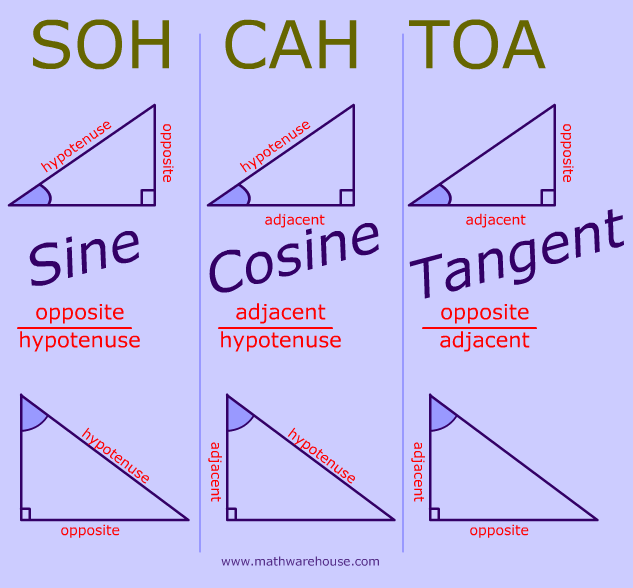
What are sin cos tan? SOHCAHTOA With Examples Teachoo Finding
A: The Sin Cos Tan formula is a set of three trigonometric ratios used to solve problems involving right triangles. The three ratios are: Sine (sin): Opposite/Hypotenuse. Cosine (cos): Adjacent/Hypotenuse. Tangent (tan): Opposite/Adjacent. What is the Trigonometry Formula Chart? A: The Trigonometry Formula Chart is a chart that shows all of the.
Sin Cos Tan Triangle Calculator Cheapest Wholesalers, Save 52 jlcatj.gob.mx
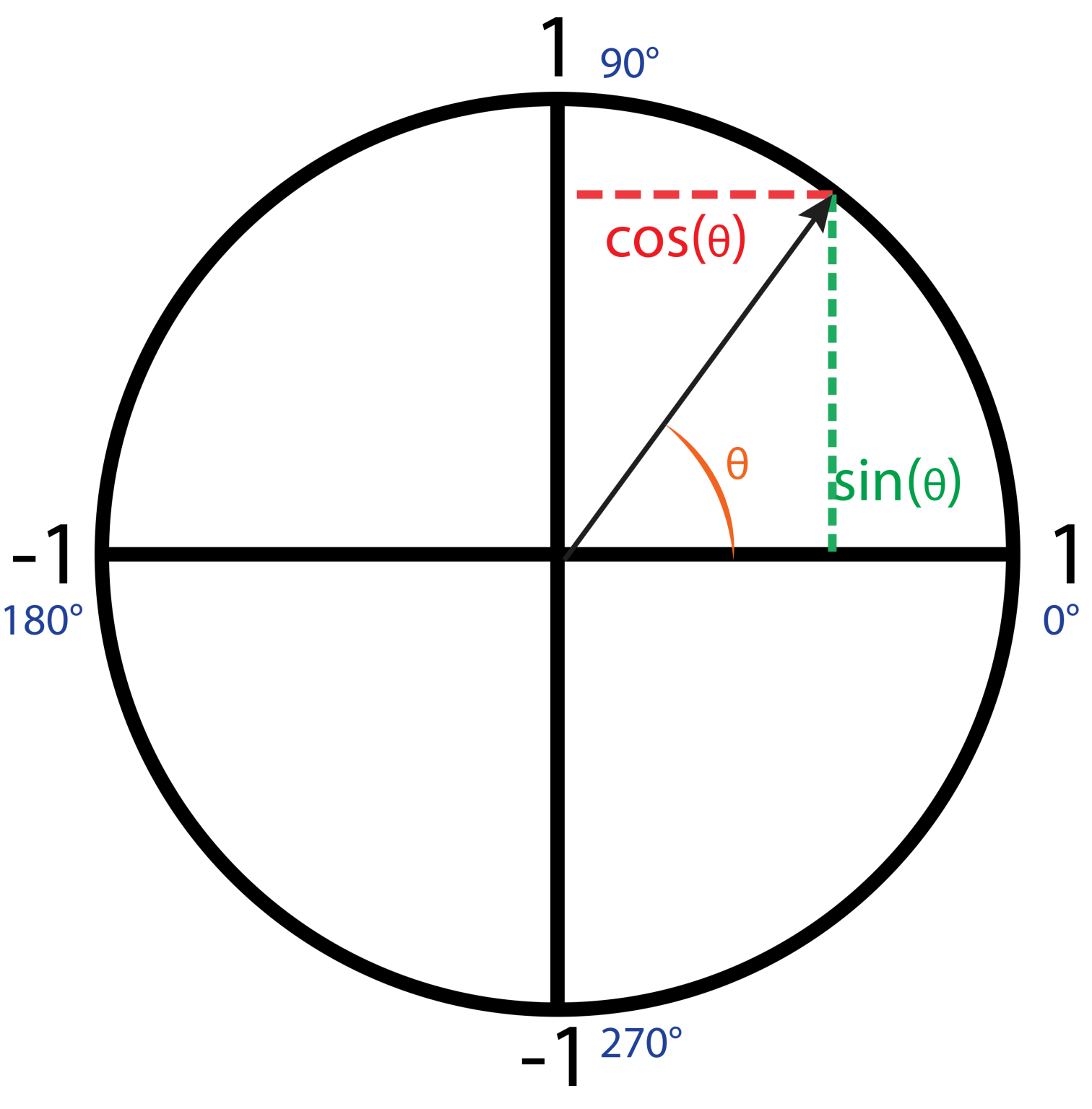
The sine of the angle = the length of the opposite side. the length of the hypotenuse. The cosine of the angle = the length of the adjacent side. the length of the hypotenuse. The tangent of the angle = the length of the opposite side. the length of the adjacent side. So in shorthand notation: sin = o/h cos = a/h tan = o/a.

sin cos tan definitions, facts and solved examples Cuemath
The important sin cos tan formulas (with respect to the above figure) are: sin A = Opposite side/Hypotenuse = BC/AB. cos A = Adjacent side/Hypotenuse = AC/AB. tan A = Opposite side/Adjacent side = BC/AC. We can derive some other sin cos tan formulas using these definitions of sin, cos, and tan functions. We know that sin, cos, and tan are the.
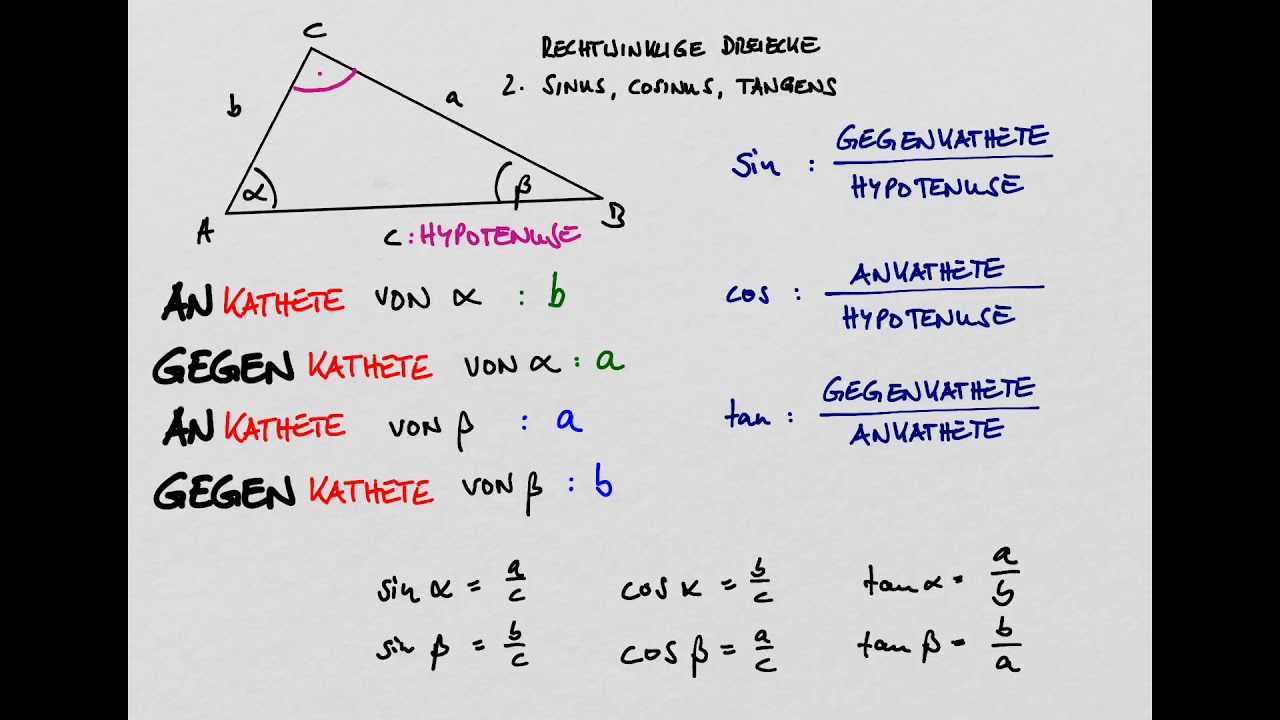
sinus cosinus tangens 2 formeln YouTube
Learn the basics of trigonometry in this video math tutorial by Mario's Math Tutoring. We discuss how to work with the trigonometric ratios: sine, cosine, a.
p5 Trigonometric functions and oscillation (sin, cos) EMS Interactivity
Here are the formulas of sin, cos, and tan. sin θ = Opposite/Hypotenuse. cos θ = Adjacent/Hypotenuse. tan θ = Opposite/Adjacent. Apart from these three trigonometric ratios, we have another three ratios called csc, sec, and cot which are the reciprocals of sin, cos, and tan respectively. Let us understand these sin, cos, and tan formulas.

Trigonometrie Sinus, Kosinus & Tangens Mehr Spicker und Erklärungen auf studes.de
The formulas of any angle θ sin, cos, and tan are: sin θ = Opposite/Hypotenuse. cos θ = Adjacent/Hypotenuse. tan θ = Opposite/Adjacent. There are three more trigonometric functions that are reciprocal of sin, cos, and tan which are cosec, sec, and cot respectively, thus. cosec θ = 1 / sin θ = Hypotenuse / Opposite.

Sin,Cos,Tan adjacent, cos, en, geometry, hypotenuse, math, sin, tan, trigonometry Glogster
Trigonometry is a branch of mathematics. The word itself comes from the Greek trigōnon (which means "triangle") and metron ("measure"). As the name suggests, trigonometry deals primarily with angles and triangles; in particular, it defines and uses the relationships and ratios between angles and sides in triangles.The primary application is thus solving triangles, precisely right triangles.

Sine, Cosine and Tangent Trigonometry, Tangent, Physics
Sin Cos Tan Formula. In order to define the formula for sin cos and tan, we make use of two of the three sides of a right-angle triangle. Let us consider the above diagram and the notations that define the hypotenuse, opposite side and the adjacent side. Sin cos tan formulas: \(\sin\theta\)= Opposite side/Hypotenuse

sin cos tan formulas
The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used.

Trigonometry, Tangent, Math methods
Sin, cos, and tan are trigonometric ratios that relate the angles and sides of right triangles. Sin is the ratio of the opposite side to the hypotenuse, cos is the ratio of the adjacent side to the hypotenuse, and tan is the ratio of the opposite side to the adjacent side. They are often written as sin (x), cos (x), and tan (x), where x is an.

Section 4 Sine And Cosine Rule
Exercise. Try this paper-based exercise where you can calculate the sine functionfor all angles from 0° to 360°, and then graph the result. It will help you to understand these relativelysimple functions. You can also see Graphs of Sine, Cosine and Tangent.. And play with a spring that makes a sine wave.. Less Common Functions. To complete the picture, there are 3 other functions where we.
What are sin cos tan? SOHCAHTOA With Examples Teachoo
What is sin cos tan? Sin cos tan is a shortened description of the three trigonometric functions of sine, cosine, and tangent.These functions associate the ratio of two sides of a right-angled triangle with an angle.. To calculate using sin, cos and tan, we need to know their trigonometric ratios (remember that the ratio of two values is a division of these values).

Trigonometry review Trigonometry, Math methods, Gcse math
Solved Examples. Question 1: Calculate the angle in a right triangle whose adjacent side and hypotenuse are 12 cm and 20 cm respectively? Solution: Given, Adjacent side = 12 cm. Hypotenuse = 20 cm. cos θ = Adjacent⁄Hypotenuse. cos θ = 12⁄20. θ = cos −1 (0.6)