Level of measurement
There are actually four different data measurement scales that are used to categorize different types of data: 1. Nominal. 2. Ordinal. 3. Interval. 4. Ratio. In this post, we define each measurement scale and provide examples of variables that can be used with each scale. Nominal. The simplest measurement scale we can use to label variables is.

PPT Chapter 1 Introduction and Data Collection PowerPoint
Level of measurement or scale of measure is a classification that describes the nature of information within the values assigned to variables. Psychologist Stanley Smith Stevens developed the best-known classification with four levels, or scales, of measurement: nominal, ordinal, interval, and ratio.

Levels of Measurement YouTube
The Different Levels of Measurement. To conclude, the levels of measurement can be either qualitative or quantitative. Qualitative data is split into two, as well. It can be nominal or ordinal, depending if there is any strict order or not. Quantitative data also consists of 2 groups - ratios and intervals. Here, the key difference is whether.

What is Nominal Data? Definition, Characteristics, Examples
Some is quantitative, and some are qualitative. Some data sets are continuous and some are discrete. Another way to separate data is to classify it into four levels of measurement: nominal, ordinal, interval and ratio. Different levels of measurement call for different statistical techniques. We will look at each of these levels of measurement.

How to Analyze Survey Results
For this level of measurement, intervals are still meaningful. Additionally, these variables have zero measurements representing a lack of the attribute. For example, zero kilograms indicates a lack of weight. Consequently, measurements ratios are valid for these scales. 30 kg is three times the weight of 10 kg. You can add, subtract, multiply.

Levels of Measurement "Nominal Ordinal Interval Ratio" Scales
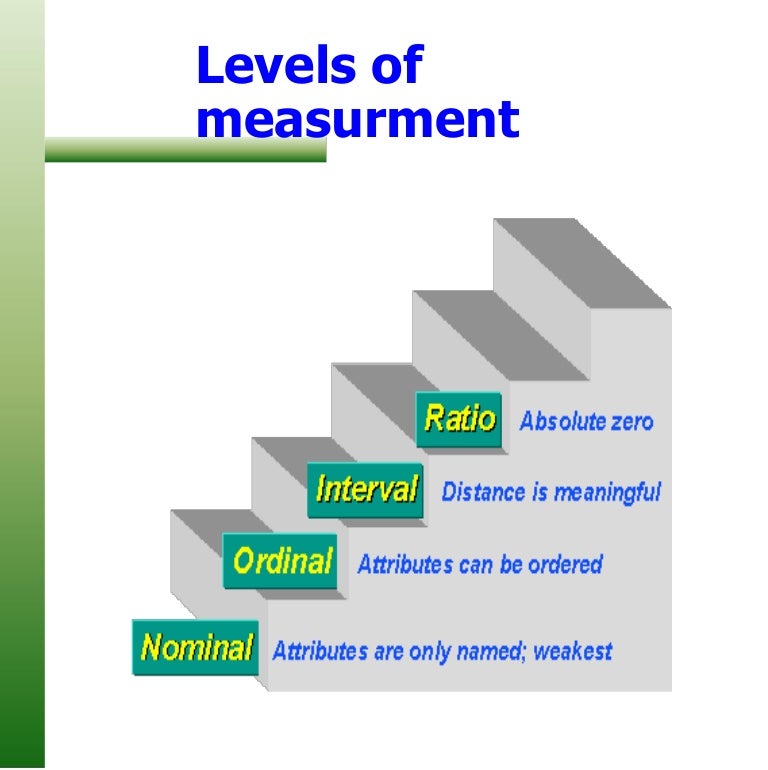
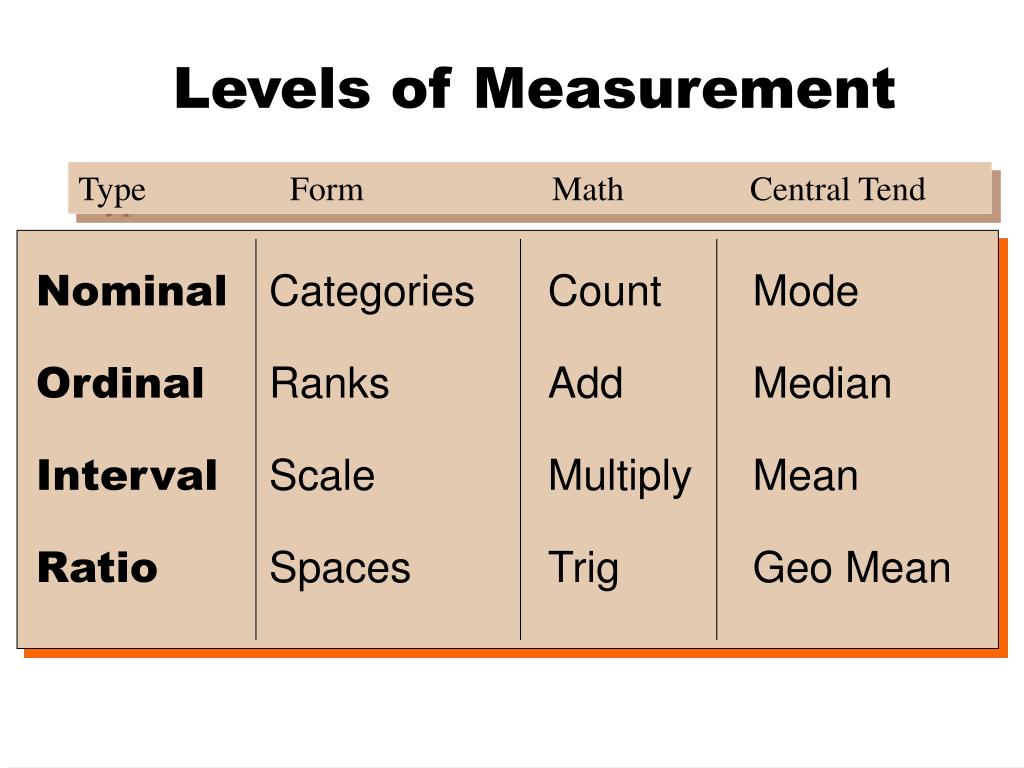
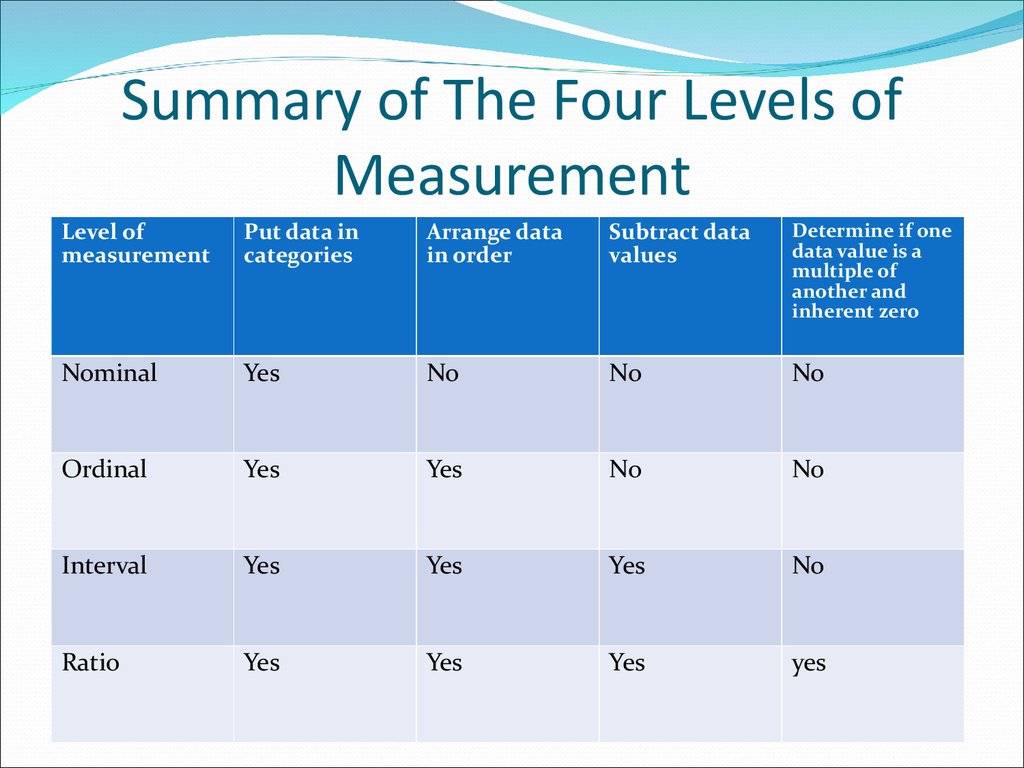
There are 4 levels of measurement: Nominal: the data can only be categorised. Ordinal: the data can be categorised and ranked. Interval: the data can be categorised, ranked, and evenly spaced. Ratio: the data can be categorised, ranked, evenly spaced, and has a natural zero. Depending on the level of measurement of the variable, what you can do.

Levels of Measurement
Levels of Measurement. The way a set of data is measured is called its level of measurement. Correct statistical procedures depend on a researcher being familiar with levels of measurement. Not every statistical operation can be used with every set of data. Data can be classified into four levels of measurement.
PPT Levels of Measurement PowerPoint Presentation, free download ID
The level of measurement is a classification used in statistics that links the values given to variables with one another. In other words, the information contained in the values is described using the level of measurement. Nominal, ordinal, interval and ratio are the four different levels of measurement.

What Is The Difference Between Nominal Ordinal Interval And Ratio
The Nominal Level of Measurement is the most fundamental form of measurement. This level categorizes or labels data without giving any quantitative value or order. It is purely qualitative and usually used for categorizing or grouping data. For example, the gender of individuals (Male, Female) represents nominal data.
Levels of measurement in statistics online statbook jordha
The crux of the matter is the relationship between the variable's level of measurement and the statistics that can be meaningfully computed with that variable. For example, consider a hypothetical study in which 5 5 children are asked to choose their favorite color from blue, red, yellow, green, and purple.

Sociology A Deeper Look Levels of Measurement
Scales of Measurement. In Statistics, the variables or numbers are defined and categorised using different scales of measurements. Each level of measurement scale has specific properties that determine the various use of statistical analysis. In this article, we will learn four types of scales such as nominal, ordinal, interval and ratio scale.
Levels of measurement Statistics with jamovi
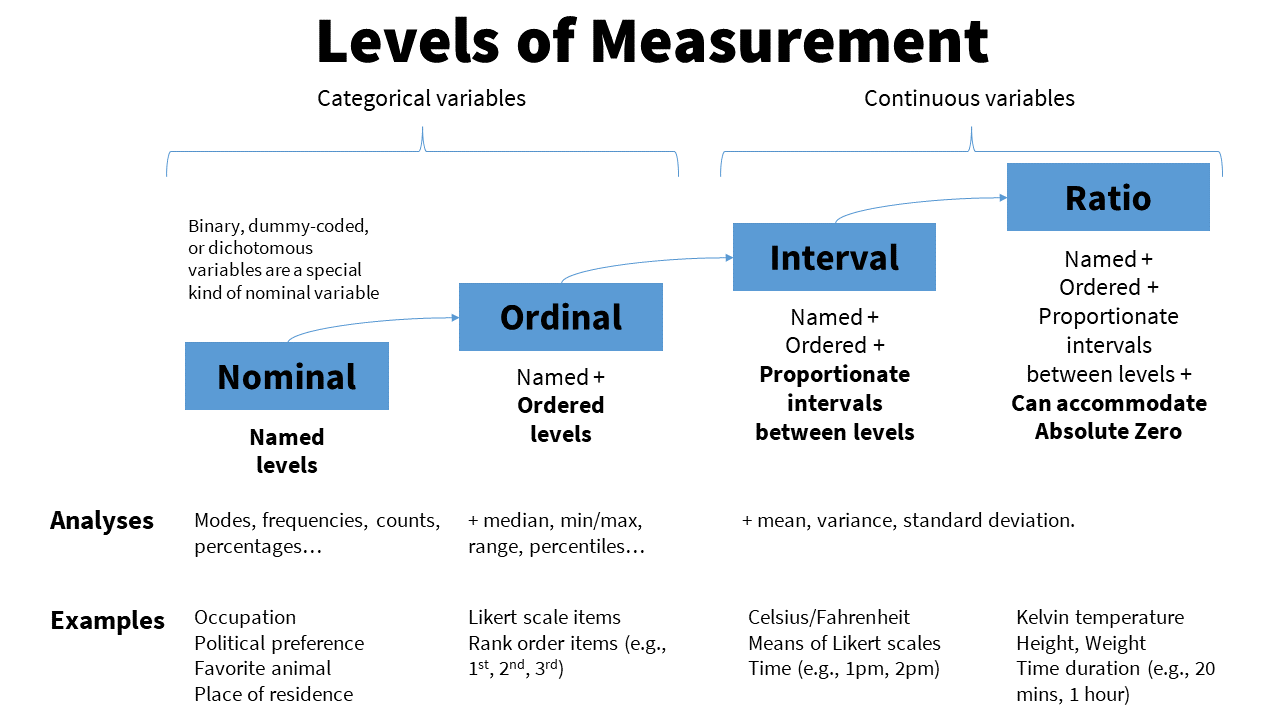
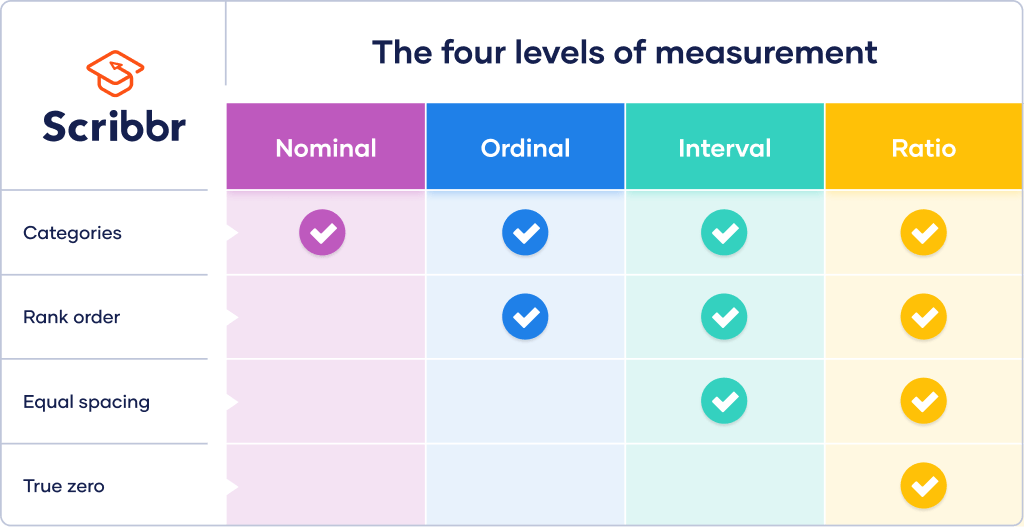
There are four types of measurement (or scales) to be aware of: nominal, ordinal, interval, and ratio. Each scale builds on the previous, meaning that each scale not only "ticks the same boxes" as the previous scale, but also adds another level of precision. The four levels of measurement displayed in a table: Nominal, ordinal, interval.

Levels Of Measure
There are 4 levels of measurement: Nominal: the data can only be categorized. Ordinal: the data can be categorized and ranked. Interval: the data can be categorized, ranked, and evenly spaced. Ratio: the data can be categorized, ranked, evenly spaced, and has a natural zero. Depending on the level of measurement of the variable, what you can do.

Nominal, Ordinal, Interval & Ratio Explained Simply Grad Coach
Nominal, Ordinal, Interval, and ratio are defined as the four fundamental measurement scales used to capture data in the form of surveys and questionnaires, each being a multiple-choice question . Each scale is an incremental level of measurement, meaning each scale fulfills the function of the previous scale, and all survey question scales.
Can Ratio Level Variables Be Discrete or Continuous Converse Milethave
4 levels of measurement. Here are the four levels of measurement that you can use to organize your data and perform a statistical analysis: 1. Nominal measurement. Nominal measurement organizes data by labeling items in mutually exclusive categories. While this level of measurement is incompatible with ordering and data calculations, it can.

PPT Chapter 1 Introduction to Statistics PowerPoint Presentation
Each level of measurement and its corresponding scale is able to measure one or more of the four properties of measurement, which include identity, magnitude, equal intervals, and a minimum value of zero. There is a hierarchy of these different levels of measurement. With the lower levels of measurement (nominal, ordinal), assumptions are.